以下是一个简单的初一有理数思维导图的Markdown格式代码:
“`markdown
# 有理数思维导图
## 有理数的定义
1. 有理数是一种有限或无限循环小数,它可以用分数表示。
2. 有理数包括整数、分数、正有理数、负有理数和零。
## 有理数的分类
### 整数
1. 正整数
2. 零
3. 负整数
### 分数
1. 正分数
2. 负分数
### 实数
1. 有限小数
2. 无限循环小数
3. 无限不循环小数
## 有理数的运算
### 加法
1. 同号两数相加,取相同的符号,并把绝对值相加。
2. 异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值。
3. 互为相反数的两数相加,得零。
4. 一个数与零相加,仍得原数。
### 减法
1. 减去一个数,等于加上这个数的相反数。
2. 对于任意实数a,a-a=0。
3. 减法中的被减数减去减数所得的差是不等于零的。
4. 当减数是大于被减数时,差的符号取决于较大的数在哪一边。
### 乘法
1. 有理数的相乘有两个因数分别相乘。即对于任意实数a、b和c,有(a × b)×c=a×(b×c)。
2. 如果两个数的积为负数,那么这两个数中至少有一个数为负数。如果两个数的和为零,那么这两个数中至少有一个数为零。这两个性质也适用于有理数的乘法运算。
3. 一个数除以一个不为零的有理数相当于这个数乘以这个数的倒数。对于任意实数a、b和c,a÷b=c⇔a×(1/b)=c。注意,0不能作为除数,即除数应为正数或零。对于分母中含有分母的概念的理解和使用应慎重。同时需要注意的是“正”或“负”只是我们的规定。有大于某个的数字就没有绝对的或无穷大之说,所以我们没必要认为分母无限大也是无穷大,是有意义而无解,并不意味着就没有“无理”。实际在生活中往往只需了解非负整数等比较具体的概念即可,负整数或正整数和负整数都属于有理数的范围,而在中学阶段有理数的范围更广泛。最后记住“分式是相对的概念,只要相对的字母不在其定义范围内就可以说是整式了。”另外初中所学的一些数学概念大部分可以借助具体题目去记忆,抽象的理解要借助思维的灵活性才能做到。注意概念的逻辑上的使用范围有助于我们记忆和使用概念。所以掌握好有理数的概念很重要。
“`
请注意,这是一个简单的思维导图代码示例,你可以根据需要对其进行修改和扩展。此外,为了在思维导图软件中查看和编辑这个思维导图,你需要将这段Markdown代码导入到支持Markdown格式导入的思维导图软件中(如XMind、MindNode等)。具体步骤可以参考所选思维导图软件的帮助文档或在线教程。

七年级上第二章
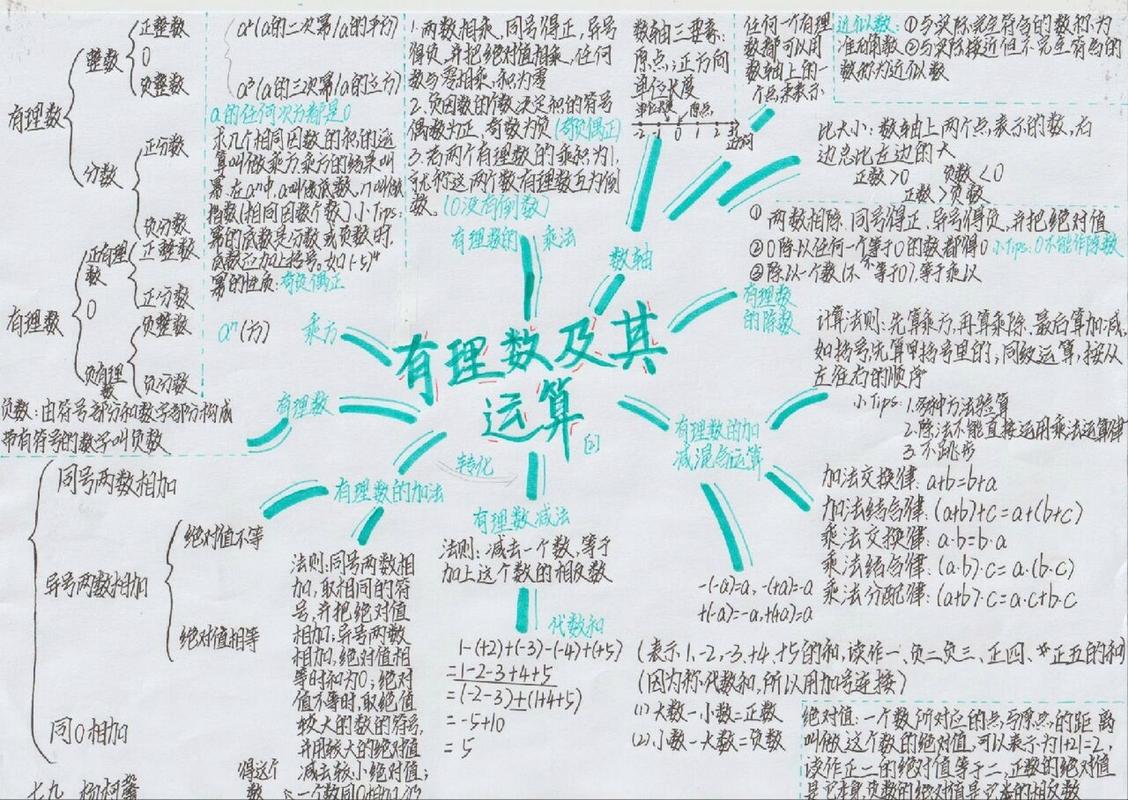
七年级数学思维导图《有理数及其运算》

初中数学人教版第一章有理数知识点思维导图

初一第二章有理数及其运算思维导图

第一章

有理数思维导图初一简单漂亮
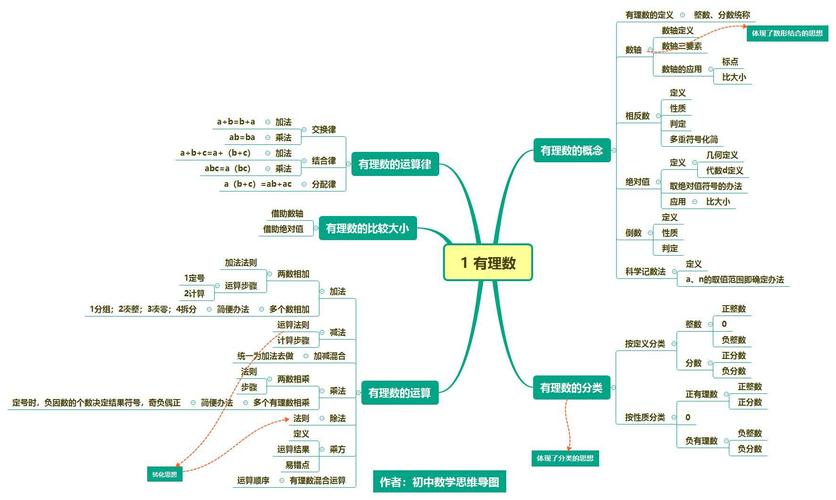
人教版七上《有理数》思维导图

七上《有理数》单元整理

《有理数》思维导图.01

七年级数学有理数(教师讲义带答案)
本文由用户 画者微云 上传分享,若内容存在侵权,请联系我们(点这里联系)处理。如若转载,请注明出处:/7988.html
